开了个新坑，准备更新一下计算机图形学课程后面的笔记。写这个的主要目的是给自己复习用，顺便发到博客上一份吧。

这篇文章主要对应的内容是二维图元的生成，包含了直线的DDA算法、中点算法、Bresenham算法，以及圆的中点算法。

---

扫描转换直线

DDA算法

DDA算法是一种最简单，最基础的直线生成的算法。简单来说，算法会 $x$ 坐标带入到直线方程中求解 $y$，随后进行四舍五入的操作。这样的算法是最简单的做法，但是它的性能开销也是巨大的。

条件

需要通过DDA算法绘制的直线需要符合以下的条件：

• 待转换的直线段：$P_0(x_0,y_0)$ $P_1(x_1,y_1)$
• 计算直线的斜率：$k=\frac{\Delta y}{\Delta x}=\frac{y_1-y_0}{x_1-x_0}$
• 计算直线的方程：$y=kx+b$
• 直线的斜率 $\left|k\right|\leq1$，如果直线的斜率 $\left|k\right|>1$，则需要将 $x,y$ 身份互换。

在完成了上述的准备工作后，可以开始DDA算法的计算了。

算法核心

由于求得了直线的方程，根据给定的一系列 $x_n$（其中 $x_i=x_{i-1}+1$），可以求得在理想直线上他所对应的 $y$ 坐标。

尽管给定的横坐标$x_i$为整数，但是由于在计算斜率的时候不可避免的会出现小数，因此通过直线的方程所求出来的纵坐标$y$的值是小数，因此需要对其进行处理，将其转换为整数。

DDA算法的核心就是对求得的$y$进行一个四舍五入的操作。其具体的实现如下：

• 划分区间：$[x_0,x_n]=x_0,x_1,x_2,…,x_i,…,x_n$，其中 $x_i=x_{i-1}+1$
• 计算纵坐标：将横坐标$x_i$带入到直线方程中，计算他的纵坐标 $y_i=kx_i+b$
• 取整：$y_{i,r}=round(y_i)=(int)(y_i+0.5)$

通过加0.5后取整数部分的方式，实现了对坐标的四舍五入的操作。

算法总结（优化）

之前的计算中需要计算直线方程的两个参数：$k$ 和 $b$。但是由于 $b$ 是固定的，其不会随着计算发生变化。通过公式推导可以发现，$y$ 可以通过递推的方式来进行计算。这样只需要求出直线的斜率$k$就可以进行后续的计算了。 $$ y_i=kx_i+b=k(x_{i-1}+1)+b=kx_{i-1}+b+k=y_{i-1}+k $$ 需要注意的是，这里的 $y$ 指的是将 $x$ 带入到直线方程后所计算的未经过取整的值。

尽管这样的方法避免了乘法运算，但是依然存在浮点数的运算。

例题

下面是一道使用DDA算法求对应的直线的坐标的例题。加粗字体的部分是题目给定的条件，常规字体的部分是需要自己填写的。

用DDA算法,扫描转换直线段$(2,1)–(5,8)$。

首先，可以求得斜率$k=\frac{8-1}{5-2}=\frac{7}{3}$。由于其斜率 $k>1$，需要将 $x,y$ 身份互换。

X	(int)(X+0.5)	Y
2	2	1
$\frac{17}{7}$	2	2
$\frac{20}{7}$	3	3
$\frac{23}{7}$	3	4
$\frac{26}{7}$	4	5
$\frac{29}{7}$	4	6
$\frac{32}{7}$	5	7
5	5	8

中点算法

在前面提到的DDA算法中，直线的斜率 $k$ 是浮点数，因此其计算出来的 $y$ 也是浮点数。但是，浮点数的计算在计算机中不利于硬件的实现。因此，中点算法是一种能够简化浮点数计算的画图算法。

条件

想要使用中点算法，存在以下的限制条件：

• 待转换的直线段：$P_0(x_0,y_0)$ $P_1(x_1,y_1)$
• 计算直线的方程：$F(x,y)=ax+by+c$，其中 $a=y_0-y_1, b=x_1-x_0, c=x_0y_1-x_1y_0$
• 直线的斜率 $k\in[0,1]$

如果直线的斜率 $k$ 不在此范围内，则需要对 $x, y$ 进行相应的变换。以下的所有内容建立在上述的条件中。

算法核心

原理

由于直线的斜率 $k\in[0,1]$，因此当每当 $x$ 增加1，$y$ 的增加幅度不会大于1。

因此，在图像上来看，假设之前的点 $Q$ 为 $(x_0, y_0)$，则对于下一个顶点 $(x_0+1,y)$ 来说，$y$ 的取值只有两种情况：$y=y_0$ 或 $y=y_0+1$。

因此和DDA算法类似的，将下一个点的中点 $M(x_0+1,y_0+0.5)$ 带入直线的方程中，就可以计算出该点相对于直线的位置了。其判别式可以写为： $$ d=F(M)=F(x_0+1,y_0+0.5)=a(x_0+1)+b(y_0+0.5)+c $$

• $d<0$ 时，则其在点 $Q$ 的上方，取 $y_0+1$ 点。
• $d>0$ 时，则其在点 $Q$ 的下方，取 $y_0$ 点。
• $d=0$ 时，则其在理想直线上，理论上任意位置均可，但是约定取 $y_0$ 点。

问题

对于每一个点，如果都需要计算判别式的值，则需要很大的性能开销。

解决方案是使用他们的增量。

优化

假设下一个点和当前点的增量为 $d$，由于下一个点存在两种可能性——右侧点或右上点，那么对于再下一个点的增量，其应该要分类讨论。

• 如果 $d\geq0$，则理想点 $M$ 在直线下方，所以取右侧的像素。这时候的增量 $d_1=F(x_p+2,y_p+0.5)=a(x_p+2)+b(y_p+0.5)+c=d+a$
• 如果 $d<0$，则理想点 $M$ 在直线上方，所以取右上侧的像素。这时候的增量 $d_2=F(x_p+2,y_p+1.5)=a(x_p+2)+b(y_p+1.5)+c=d+a+b$

$d$ 的增量确定了，接下来需要确定他的初始值 $d_0$。 $$ d_0=F(x_0+1,y_0+0.5)=F(x_0,y_0)+a+\frac{1}{2}b $$ 由于 $F(x_0,y_0)$ 在直线上，因此 $F(x_0,y_0)=0$，所以 $d_0$ 可以写为： $$ d_0=a+\frac{1}{2}b $$ 尽管 $a$ 和 $b$ 都是整数，但是由于出现了非整数的系数，这会导致 $d_0$ 变回浮点数，从而拖慢计算。由于我们在使用 $d$ 的时候实际上只在乎其与0的关系，其数值部分其实并不重要。

因此，我们在计算的时候，统一的将增量乘2，用这样的数值来进行计算。这样就避免了浮点数的运算。

算法总结

因此，经过处理，中点算法的增量如下：

• 初始值 $d_0=a+a+b$
• $d\geq0$ 时，取右侧的像素。增量为 $d_1=a+a$。
• $d<0$ 时，取右上侧的像素。增量为 $d_2=a+a+b+b$。

Bresenham算法

这是计算机图形学中最常用的直线扫描算法。其总体的思想类似于中点算法，但是其只有一个增量。

条件

• 假设直线的方程为 $y_{i+1}=y_i+k(x_{i+1}-x_i)$，由于 $x$ 的增量为1，因此 $y_{i+1}=y_i+k$。
• $k=\frac{dy}{dx}=\frac{y_1-y_0}{x_1-x_0}$
• 直线的斜率 $k\in[0,1]$

算法核心

算法的核心也是需要去构造误差，来不断的更新。假设起始点 $(x_0,y_0)$，则下一个点 $(x_0+1,y)$ 中的 $y$ 有两种取值：$y=y_0$ 或 $y=y_0+1$。判断 $y$ 的取值，需要根据 $d$ 的数值来判断。

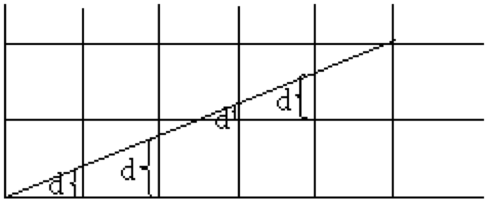
由于起始点在直线上，他的偏差是0。因此，$d_0=0$。

由上图可见，很显然，如果 $d\geq0.5$，则其更加接近靠上的像素点；反之，则更靠近下面的像素点。

为了减少浮点数的计算，方便计算，可以令 $e=d-0.5$。根据直线的斜率的定义可知道，随着 $x$ 增大1，$y$ 增大的数值为 $k$。

所以总结来说，$e_0=-0.5$，增量为 $k$。每一次进行计算的时候，$e\gets e+k$

• 如果 $e\geq0$ 时，取 $(x_0+1,y_0+1)$，同时 $e\gets e-1$
• 如果 $e<0$ 时，取 $(x_0+1,y_0)$

算法总结（优化）

给予和中点法类似的理由，Bresenham法也只需要通过误差项的符号来判断像素的取法。因此，其误差项的赋值如下：

• 初值 $e_0=-dx$
• 增量 $e^+=2dy$
• 减量 $e^-=2dx$

扫描转换圆弧

由于圆具有对称性，因此只需要绘制 $\frac{1}{8}$ 个圆弧，就可以通过水平、垂直、对角线这三种变换来得到一个完整的圆形。

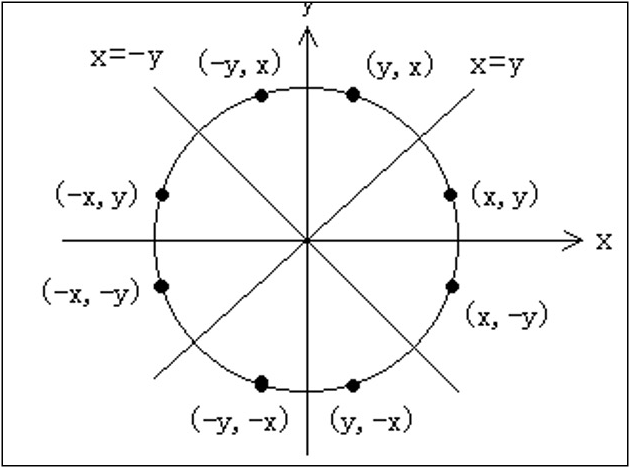
上图展示的是圆在不同的象限内所对应的坐标。

绘制圆的方法有很多，两种直接绘制的方法是使用离散点或参数方程的方式，直接求出他们的坐标进行绘制。但是无论使用三角函数或者进行根号运算，都需要大量的系统资源占用。因此，在实际绘制中，不会使用这样的方法。

中点算法

圆弧的中点算法和直线的中点算法类似。同样的，因为圆具有对称性，因此只需要进行多次翻转就可以完成图形的绘制。因此，在这里只考虑 $\frac{1}{8}$ 个圆。

条件

假设圆的中点在原点，并且圆的半径已知。圆弧的隐函数可以写为： $$ f(x,y)=x^2+y^2-R^2=0 $$ 显然，如果一个点在圆弧外，则 $f(x,y)>0$；一个点在圆弧内，则 $f(x,y)<0$。

算法核心

原理

这里考虑第一象限的上部分的圆，这部分圆的切线斜率 $k\in[-1,0]$。

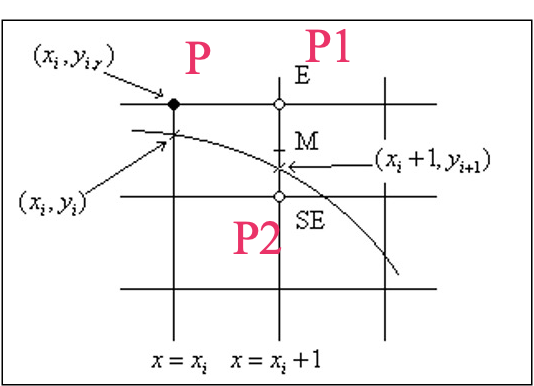
因此，如果给定了 $P(x_i,y_i)$ 的坐标，对于 $P^{’}(x_i+1,y_{i+1})$ 来说，他的纵坐标有两种取值方法：$y_{i+1}=y_i$ 或 $y_{i+1}=y_i-1$。

因此，我们取他们的中点 $M(x_i+1,y_i-0.5)$，并且把这个点带入到圆的隐函数方程中，判断其是否在圆的内部。

• 如果判别式 $F(x,y)>0$，则说明中点在圆的外部，选择右下点 $P_2$
• 如果判别式 $F(x,y)<0$，则说明中点在圆的内部，选择右侧点 $P_1$。

总结

构造判别式： $$ d=f(M)=f(x_p+1,y_p-0.5)=(x_p+1)^2+(y_p-0.5)^2-R^2 $$

• 如果 $d<0$，取正右侧的点，再下一个像素的判别式为：$d_1=f(x_p+2,y_p-0.5)=d+2x_p+3$。
• 如果 $d>0$，取右下方的点，再下一个像素的判别式为：$d_2=f(x_p+2,y_p-1.5)=d+2(x_p-y_p)+5$。
• 初始值 $d_0=F(1,R-0.5)=1.25-R$

优化

这里同样存在浮点数。因此，需要将浮点数运算尽可能的消去。我们可以将 $d$ 用 $e=d-0.25$ 来替代。这样以后，增量为：

• 初始值 $e_0=1-R$
• 如果 $e<0$，则 $e_1=2x+3$
• 如果 $e>0$，则 $e_2=2(x-y)+5$