直线段裁剪

在使用计算机处理图形信息时，计算机内部存储的图形往往比较大，而屏幕显示的只是图的一部分。因此需要确定图形中哪些部分落在显示区之内，哪些落在显示区之外，以便只显示落在显示区内的那部分图形。这个选择过程称为裁剪。

• 目的：判断图形元素是否落在裁剪窗口之内并找出其位于内部的部分
• 基础：图元关于窗口内外关系的判别；图元与窗口的求交
• 条件：裁剪窗口：$[x_\min, x_\max] \times [y_\min,y_\max]$

直线与显示区的关系可以归类为以下三种：

1. 直线完全可见：即两个端点都在窗口中
2. 显然不可见：两个端点都在窗口某条边所在直线的外侧
3. 线段至少有一个端点在外部，但是不是显然不可见

在设计算法的时候，前两种情况都是相对比较好处理的。但是对于第三种情况，需要对线段与窗口的交点坐标进行求解，才能够确定直线的具体位置。这个过程需要耗费更多的资源，应该尽可能的避免。

对于点是否在窗口内部，这是他的充分必要条件： $$ x_\min \le x \le x_\max\ y_\min \le y \le y_\max $$ 满足了这个条件，就可以说这个点是在窗口内部的。

直接求交算法

直接求交法的核心思想是将直线与窗口边都写成参数形式，求解参数值。

这导致了他算法本身并不难，但是当程序在判断属于哪种情况的时候，计算会很复杂。他的流程图可以如下图所示。

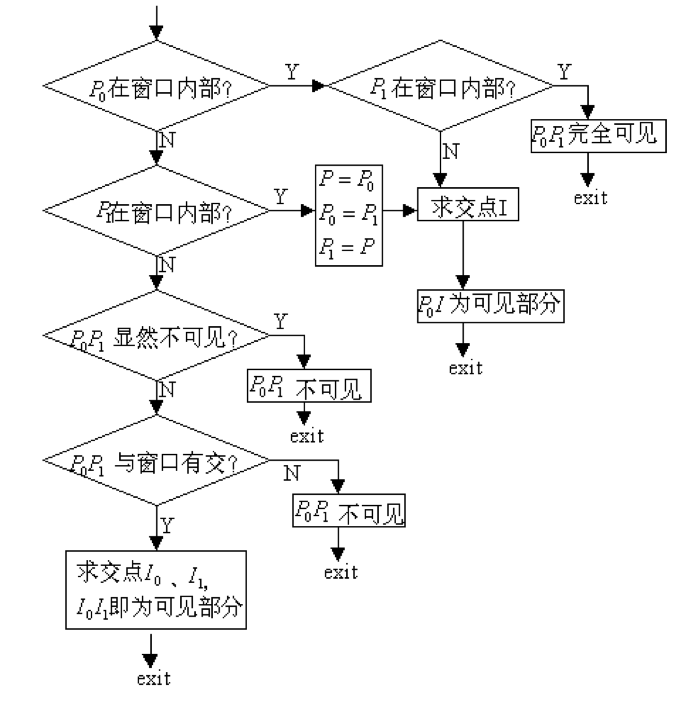
Cohen-Sutherland 算法（编码算法）

算法步骤

1. 判别线段两端点是否都落在窗口内。如果是，则线段完全可见；否则进入下一步。
2. 判别线段是否为显然不可见。如果是，则裁剪结束；否则进行下一步 。
3. 求线段与窗口边延长线的交点，这个交点将线段分为两段，其中一段显然不可见，丢弃。对余下的另一段重新进行第一步，第二步判断，直至结束。

编码

定义

为了更快的判断点是否在窗口内，C-S算法对窗口的各个区域进行了编码。

由窗口四条边所在直线把二维平面分成9个区域，每个区域赋予一个四位编码。编码的格式是 $C_tC_bC_rC_l$ ，分别对应的是上下右左。

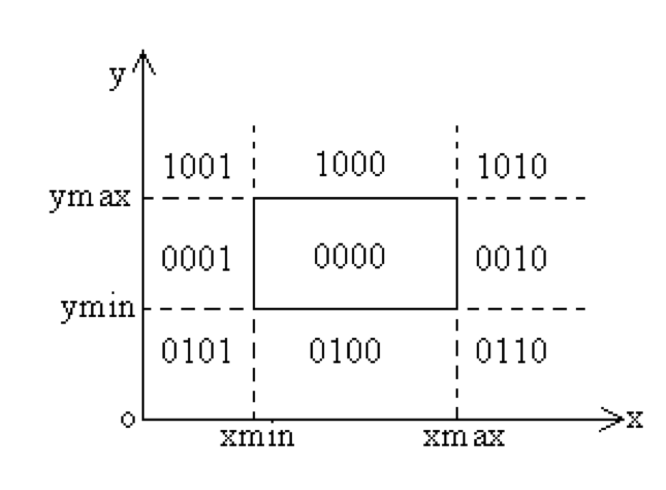
其中， $C_tC_bC_rC_l$ 的编码格式如下： $$ C_t=\left{ \begin{aligned} 1 && 当y>y_\max\ 0 && else\ \end{aligned} \right. $$

$$ C_b=\left{ \begin{aligned} 1 && 当y<y_\min\ 0 && else\ \end{aligned} \right. $$

$$ C_r=\left{ \begin{aligned} 1 && 当x>x_\max\ 0 && else\ \end{aligned} \right. $$

$$ C_l=\left{ \begin{aligned} 1 && 当x<x_\min\ 0 && else\ \end{aligned} \right. $$

通过这样的方式，就可以对任意区域上的端点都进行编码了。有了这些编码以后，就可以开始判断直线的关系了。

判别

• 完全可见：两个端点的编码是否都为0000
• 显然不可见：两个端点的编码求逻辑与，判断是否不是0000
• 需要求交的线段：两个端点的编码求逻辑或，如果某一条边的编号为1，则需要计算与这条边的交点

算法评价

• 特点：用编码方法可快速判断线段–完全可见和显然不可见。
• 适合场景：大窗口场合（大多数对象都在窗口中）；窗口特别小的场合（如光标拾取图形时，光标看作小的裁剪窗口。)
• 最坏情况：直线与窗口存在4个交点

参考代码

#define LEFT 1
#define RIGHT 2
#define BOTTOM 4
#define TOP 8

int encode(float x, float y, float XL, float XR, float YB, float YT) { //  计算点x, y的编码
    int c = 0;
    if (x < XL) c |= LEFT; // 置位CL
    if (x > XR) c |= RIGHT; // 置位CR
    if (x < YB) c |= BOTTOM; // 置位CB
    if (x < YT) c |= TOP; // 置位CT
    return c;
}

//(x1,y1)(x2,y2)为线段的端点坐标，其他四个参数定义窗口的边界
void CS_LineClip(float x1, float y1, float x2, float y2, float XL, float XR, float YB, float YT) {
    float x, y;
    int code1, code2, code;
    // 端点坐标编码
    code1 = encode(x1, y1, XL, XR, YB, YT);
    code2 = encode(x2, y2, XL, XR, YB, YT);
    // 直到”完全可见”为止
    while (code1 != 0 || code2 != 0) {
        // 排除”显然不可见”情况
        if ((code1 & code2) != 0)
            return;
        code = code1;
        // 求得在窗口外的点
        if (code1 == 0)
            code = code2;
        // 按顺序检测到端点的编码不为0，才把线段与对应的窗口边界求交。
        if ((LEFT & code) != 0) { // 线段与窗口左边延长线相交
            x = XL;
            y = y1 + (y2 - y1) * (XL - x1) / (x2 - x1);
        } else if ((RIGHT & code) != 0) { // 线段与窗口右边延长线相交
            x = XR;
            y = y1 + (y2 - y1) * (XR - x1) / (x2 - x1);
        } else if ((BOTTOM & code) != 0) { // 线段与窗口下边延长线相交
            y = YB;
            x = x1 + (x2 - x1) * (YB - y1) / (y2 - y1);
        } else if ((TOP & code) != 0) { // 线段与窗口上边延长线相交
            y = YT;
            x = x1 + (x2 - x1) * (YT - y1) / (y2 - y1);
        }
        if (code == code1) { //裁去P1到交点
            x1 = x;
            y1 = y;
            code1 = encode(x, y);
        } else {  //裁去P2到交点
            x2 = x;
            y2 = y;
            code2 = encode(x, y);
        }
    }
    drawLine(x1, y1, x2, y2);
}

中点分割法

算法概述

与C-S算法相同，首先对线段端点进行编码，并把直线分成三种情况：全在窗口内部、完全不在窗口内部和线段和窗口有交。

针对前两种情况，使用C-S方法的处理方式。对于最后一种情况，用中点分割的方法求出线段与窗口的交点。

简单来说，其实从两个顶点出发，寻找最近的可见点。这两个可见点的连线就是可见的直线部分。

算法步骤

1. 计算出 $P_0P_1$ 的中点 $P_m$
2. 计算 $P_0$ 和 $P_m$ 的区域码的按位与。如果结果等于0，说明最近可见点在 $P_0P_m$ 上，取 $P_0P_m$ 代替 $P_0P_1$ ；否则取 $P_mP_1$ 代替 $P_0P_1$ ；
3. 如果 $P_mP_1$ 的长度小于给定的容差，即$|P_1P_m|<\epsilon$，则进入下一步；否则回到第一步。
4. 结果输出：$P_m$ 就是 $P_0$ 的最近可见点，算法结束。

由于该算法的主要计算过程只用到加法和除2运算，所以特别适合硬件实现。

多边形裁切

多边形裁切的核心难点有以下两点：

1. 多边形是一个封闭区域，裁剪后仍应当是封闭的多边形。但是多边形的边被裁剪后一般不再封闭了，需要用窗口边的适当部分来封闭它。那么，如何选择这适当部分？

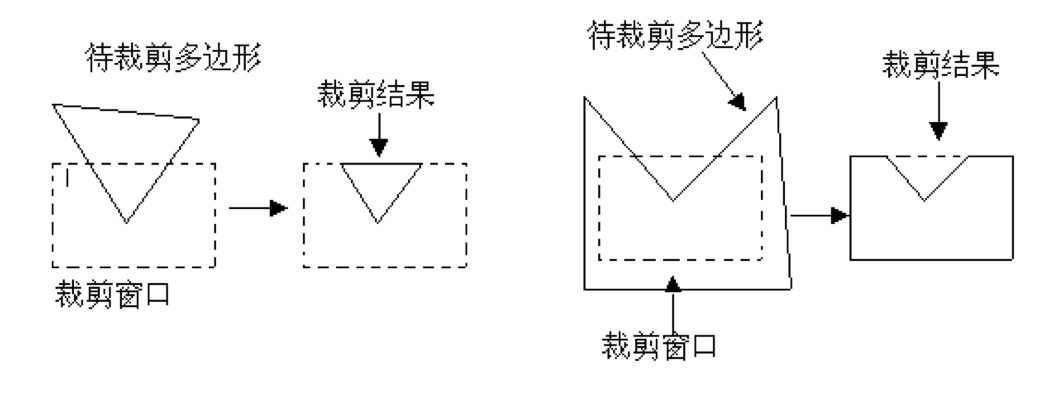
1. 一个凹多边形可能被裁剪成几个小的多边形，如何确定这些小多边形的边界？

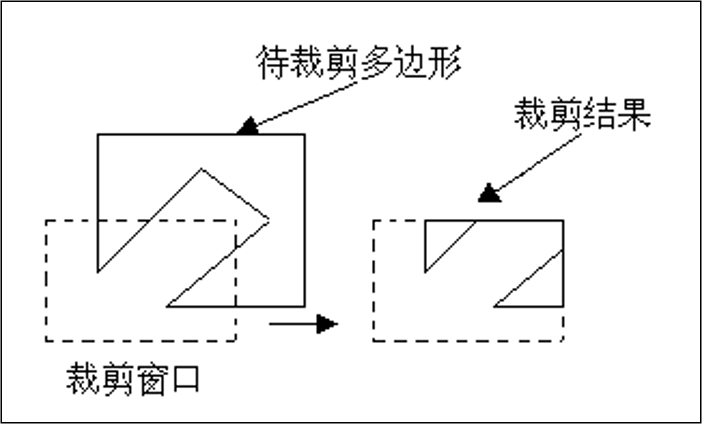
Sutherland-Hodgman算法（逐边裁剪算法）

算法概述

• 采用分割处理策略：将多边形关于矩形窗口的裁剪分解为多边形关于窗口四边所在直线的裁剪。
• 使用流水线过程（顺序：左上右下）：左边裁剪结果是上边裁剪的输入

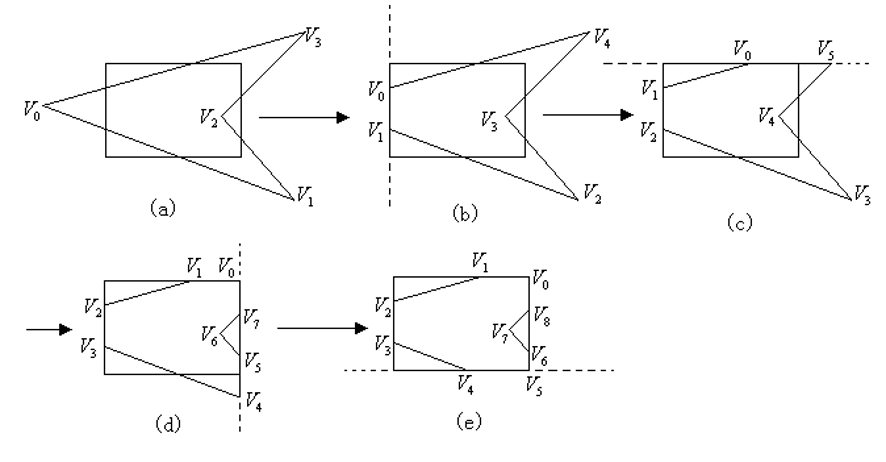
算法步骤

窗口的边及其延长线可以把区域划分成两个部分：

• 包含窗口的部分称为内侧空间
• 不包含窗口的部分称为外侧空间

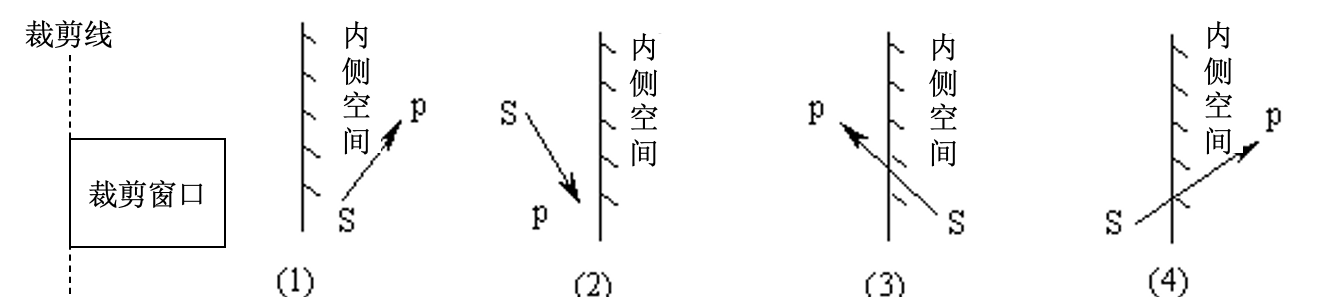
依序考虑多边形的各条边的两端点S和P：它们与裁剪线的位置关系只有四种。

1. S和P均在内侧
2. S和P均在外侧
3. S在内侧，P在外侧
4. S在外侧，P在内侧

由于现在考虑的多边形的其中一条边，端点S在上一轮已经处理过了，这里就不再考虑S点。

当前线段端点S、P与裁剪线比较之后，可输出0至2个顶点。这同样需要根据点与裁切线的关系来分类讨论：

1. 只输出P点
2. 不输出端点
3. 只输出SP与裁切线的交点
4. 输出SP与裁切线的交点、P点

通过这样的方式，我们获得了一个顶点集，接下来将他们依次相连，就形成了最后的多边形了。

算法总结

说明：

1. 裁剪算法采用流水线方式，适合硬件实现。
2. 可推广到任意凸多边形裁剪窗口。只需要对任意多边形窗口的每一条边都重复这样的操作即可。

使用范围：

• 适用于裁剪凸多边形。
• 适用于裁剪后只有一个多边形的凹多边形。

局限：

• 问题：如果裁剪后的凹多边形有分离部分出现（结果多边形多于一个），这时会出现多余的线。
• 解决方案：将凹多边形分割成2个或多个凸多边形分别进行处理。