二维基本变换

平移变换

假设点 $P(x,y)$ 。其在 $x$ 轴的平移距离为 $t_x$ ，在 $y$ 轴的平移距离为 $t_y$。得到 $P^\prime (x^\prime,y^\prime)$ ，则他们的坐标的关系可以表示为：

$$ x^\prime=x+t_x $$

$$ y^\prime=y+t_y\ $$

如果使用矢量的形式来表示的话，可以写为：

$$ P^\prime=P+T $$

其中，符号$P^\prime, P, T$的定义如下：

$$ P^\prime=\left[ \begin{matrix} x^\prime\ y^\prime \end{matrix} \right] \qquad P=\left[ \begin{matrix} x\ y \end{matrix} \right] \qquad T=\left[ \begin{matrix} t_x\ t_y \end{matrix} \right] $$

旋转变换

使用极坐标，可以简单的进行旋转变换。只需要将原来的角度加上新增的旋转角度增量，就可以完成坐标的变换了。不过，在计算机图形学中，大部分情况下使用的还是直角坐标。不过，这不影响我们推导旋转变换的矢量公式。

假设点 $P(x,y)$ 。使用极坐标表示，他的坐标可以写为： $$ x=r\cos \phi $$

$$ y=r \sin \phi\ $$

假设点 $P$ 绕坐标原点旋转角度 $\theta$ （逆时针为正），得到 $P^\prime(x^\prime, y^\prime)$ ，则他们的坐标关系可以写为：

$$ x^\prime=r\cos (\phi+\theta) $$ $$ y^\prime=r\sin (\phi+\theta) $$ $$ x^\prime=r\cos\phi\cos\theta-r\sin\phi\sin\theta $$ $$ y^\prime=r\cos\phi\sin\theta+r\sin\phi\cos\theta $$ $$ x^\prime=x\cos\theta-y\sin\theta $$ $$ y^\prime=x\sin\theta+y\cos\theta $$ 因此，将他转换为矢量的形式可以写为： $$ P^\prime=RP $$ 其中： $$ P^\prime=\left[ \begin{matrix} x^\prime\ y^\prime \end{matrix} \right] \qquad R=\left[ \begin{matrix} \cos\theta & -\sin\theta\ \sin\theta & \cos\theta \end{matrix} \right] \qquad P=\left[ \begin{matrix} x\ y \end{matrix} \right] $$

缩放变换

假设点 $P(x,y)$ 。其在 $x$ 轴方向上缩放了 $s_x$ 倍，在 $y$ 轴方向上缩放了 $s_y$ 倍。得到 $P^\prime (x^\prime,y^\prime)$ ，则他们的坐标的关系可以表示为： $$ x^\prime=s_xx $$ $$ y^\prime=s_yy $$ 他的矢量形式可以写为： $$ P^\prime=SP $$ 其中： $$ P^\prime=\left[ \begin{matrix} x^\prime\ y^\prime \end{matrix} \right] \qquad R=\left[ \begin{matrix} s_x & 0\ 0 & s_y \end{matrix} \right] \qquad P=\left[ \begin{matrix} x\ y \end{matrix} \right] $$ 他的缩放是以原点为中心的。

齐次坐标

从之前的矢量形式可以看到，旋转变换和缩放变换使用的都是矩阵乘法的形式。因此，其是具有结合率的，可以直接复合。例如，如果一个图形先旋转再缩放，他的最后坐标的矩阵可以写为： $$ P^{\prime\prime}=SP^{\prime}=S(RP)=(SR)P $$ 但是，由于平移变换使用的是矩阵的加法，不能使用结合率。他不能像这样复合。

因此，齐次坐标被提出来，从而使各种转换的表示形式一致，使变换合成更加容易。

定义

$(x,y)$ 点所对应的齐次坐标为 $(x_h, y_h,h)$ ，其中：$x_h=hx,;y_h=hy,;h\ne0$ 。

一个点的齐次坐标表示并不唯一，且他对应的齐次坐标是三维空间的一条直线： $$ \left{ \begin{aligned} x_h=hx\ y_h=hy\ z_h=h\ \end{aligned} \right. $$ 为了运算简单，引入了标准齐次坐标 $(x,y,1)$ 。

总结

再次观察前面的三种变换的变换矩阵，可以发现一定的规律。我们可以按下图把齐次变换矩阵分割成下面四个区域。

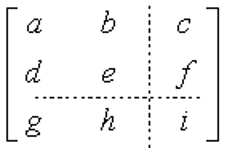
• 左上角(a,b,d,e)区域可以对图形进行缩放、旋转、对称、错切等变换。
• 右上角(c,f)区域可以对图形进行平移变换。
• 左下角(g,h)区域可以对图形作投影变换。
• 右下角(i)区域可以对图形做整体的缩放变换。

复合变换

由于现在所有的运算都使用了矩阵的乘法来实现了，根据矩阵乘法的结合率，可以将多个变换进行复合。

不过需要注意的是，由于矩阵的乘法没有交换律，对于一些顺序不可交换的变换，务必把先进行的变换写在右边，后进行的变换写在左边。

除此以外，下面介绍的三个基本变换都是以原点为中心的。如果想要以任意点为中心的，需要先使用平移变换，把任意点变成原点，做缩放或旋转变换，再平移回去。